Software Engineer

5 minute read

在这篇文章中，我们将使用PyTorch实现Qwen3。

1. 模型结构

Qwen3模型的整体架构如下图所示(图片来自Sebastian Raschka的Blog)

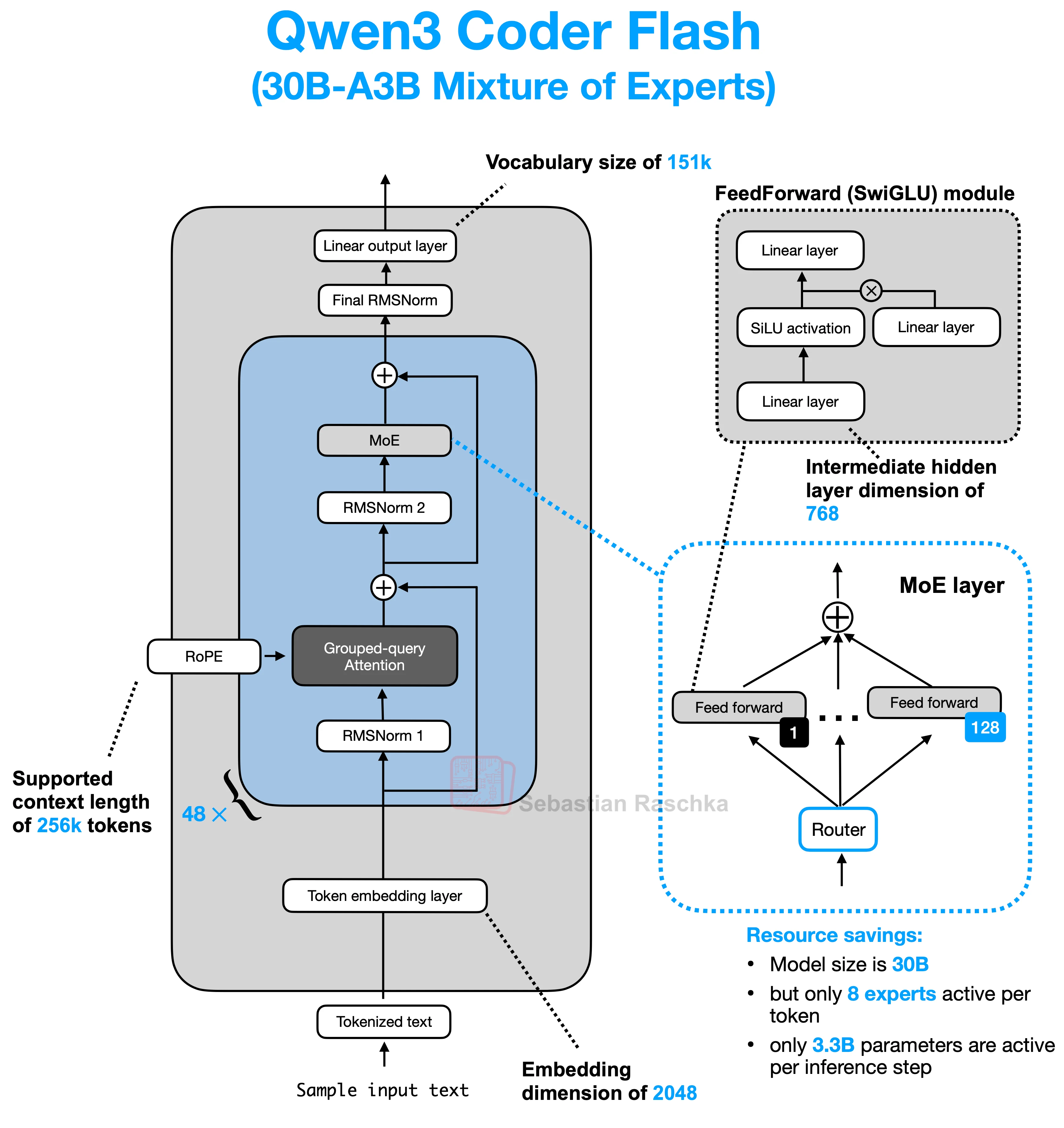
Qwen3 Architecture

可以看到Qwen3模型主要包含以下几个部分

  • Tokenization: 将input text转化为token
  • Token Embedding: 将token转化为一定维度的向量
  • Transformers: 核心计算模块，包含48个Transformer Block
    • RMSNorm: 输入首先会进行layer normalization
    • Attention Mechanism:
      • Grouped-query Attention: 使用GroupedQueryAttention替代原始的MultiHeadAttention实现自注意力机制，可以减少计算量
      • RoPE: 位置编码，用于将token的相对位置信息编码到向量中
    • Mixutre of Experts
      • FeedForward(SwiGLU): 使用SwiGLU作为激活函数
      • MoE Layer: 使用MoE来混合融合多个专家，每个专家都是一个FeedForward(SwiGLU)，在推理时会激活不同的专家，从而实现混合专家的计算并减少计算量
  • RMSNorm: 最终的归一化层, 用于稳定训练
  • Linear Output: 将输入向量由内部的维度映射到词汇表上，得到最终的logits

在下一节中我们将使用PyTorch来实现Qwen3的各个模块

2. 构建模块

2.1. RMSNorm

RMSNorm是对原始Layer Normalization的一种简化，在不影响最终效果的情况下稳定训练，公式如下

\(\text{RMS}(x) = \sqrt{\frac{1}{N} \sum_{i=1}^{N} x_i^2}\) \(y = \frac{x}{\text{RMS}(x) + \epsilon} \cdot g\)

其中:

  • (x) 是输入向量
  • (N) 是向量 (x) 的维度大小
  • (epsilon) 是一个很小的平滑项，用来避免分母为零
  • (g) 是一个可学习的缩放参数，与 (x) 的形状相同

使用PyTorch的实现如下

class RMSNorm(torch.nn.Module):
    def __init__(self, emb_dim: int, eps=1e-6, bias=False):
        super().__init__()
        self.eps = eps
        self.scale = torch.nn.Parameter(torch.ones(emb_dim))
        self.shift = torch.nn.Parameter(torch.zeros(emb_dim)) if bias else None

    def forward(self, x):
        variance = x.pow(2).mean(-1, keepdim=True) + self.eps
        norm = x * torch.rsqrt(variance)

        norm = norm * self.scale
        if self.shift:
            norm = norm + self.shift

        return norm

2.2. Rotary Positional Embeddings(RoPE)

RoPE是一种位置编码方式，目标是给Transformer提供位置信息，同时保持良好的相对位置建模能力。

Transformer模型本身没有顺序的概念，它的输入是一个或多个token序列，因此需要通过位置编码来提供位置信息。在GPT2模型中，作者使用了绝对位置编码，也就是将每个token的位置索引作为一个categorical的信息，之后再使用embedding layer将其转化为高维向量，与token embedding相加之后作为Transformer的输入。

不过绝对位置编码存在一些问题。首先这些编码对于特定长度的输入是固定的，不能很好地处理训练时未见过的序列长度；其次它只提供了序列的全局绝对位置信息，无法直接捕获相对位置关系。

RoPE尝试解决这些问题，它将位置编码”旋转”地注入到注意力机制中，以建模token之间的相对位置信息。假设我们有一个d维的向量，RoPE的做法是将向量划分成一对一对的二维向量，比如

\[x = [x1, x2, x3, x4, ..., xd-1, xd] → [(x1, x2), (x3, x4), ...]\]

然后这些二维对左旋转变换，每对(xi, xi+1)被乘以一个与位置相关的旋转矩阵

RoPE(x, pos) = Rotate(x, θ_pos)

其中旋转角度与位置pos有关。

使用RoPE得到的结果与相对位置有关，也就是说Q在位置m=1时，对K在位置n=2的注意力得分与Q在位置m=3时，对K在位置n=4的注意力得分应该是相同的。

具体实现需要两个函数

def get_sin_cos(pos_seq_len, dim):
    half_dim = dim // 2

    # shape: (half_dim,)
    theta = 1.0 / (10000 ** (torch.arange(0, half_dim, dtype=torch.float32) / half_dim))

    # shape: (pos_seq_len, 1)
    position = torch.arange(pos_seq_len, dtype=torch.float32).unsqueeze(1)

    # shape: (pos_seq_len, half_dim)
    angle = position * theta.unsqueeze(0)

    # shape: (pos_seq_len, 1, half_dim)
    sin = torch.sin(angle).unsqueeze(1)
    cos = torch.cos(angle).unsqueeze(1)

    return sin, cos


def apply_rotary_pos_emb(x, sin, cos):
    """Apply rotary position embedding to the input tensor.

    Args:
        x (torch.Tensor): Input tensor of shape (batch_size, seq_len, num_heads, head_dim)
        sin (torch.Tensor): Sinusoidal position embedding of shape (seq_len, 1, d_model)
        cos (torch.Tensor): Cosinusoidal position embedding of shape (seq_len, 1, d_model)
    """
    # shape: (batch_size, seq_len, num_heads, half_dim)
    x1 = x[..., ::2]
    x2 = x[..., 1::2]

    # shape: (batch_size, seq_len, num_heads, head_dim)
    x_rotated = torch.cat([x1 * cos - x2 * sin, x1 * sin + x2 * cos], dim=-1)
    return x_rotated

其中get_sin_cos函数用于生成sin和cos值，apply_rotary_pos_emb函数用于将sin和cos值应用到输入向量上。

2.3. Grouped Query Attention(GQA)

在论文Attention Is All You Need中，作者提出了原始的MultiHeadAttention，即利用多组不同的Query, Key和Value矩阵来计算注意力，最后将来自不同组的结果stack起来得到最终的输出。之后的GPT2等模型也都使用了MultiHeadAttention。

GroupedQueryAttention是对原始MultiHeadAttention的一种改进，在计算注意力时，将Key和Value矩阵分成多组，每组使用不同的Key和Value矩阵来计算注意力，和MultiHeadAttention相比，GroupedQueryAttention同一个group中的head可以共享Key和Value矩阵，从而减少总体的计算量。

import torch
from rms_norm import RMSNorm
from rope import apply_rotary_pos_emb


class GroupedQueryAttention(torch.nn.Module):
    def __init__(
        self,
        d_in: int,
        num_heads: int,
        num_kv_groups: int,
        head_dim=None,
        qk_norm=None,
    ):
        super().__init__()

        assert (
            num_heads % num_kv_groups == 0
        ), "num_heads must be divisible by num_kv_groups"

        self.num_heads = num_heads
        self.num_kv_groups = num_kv_groups
        self.group_size = num_heads // num_kv_groups

        self.head_dim = d_in // num_heads
        self.d_out = num_heads * head_dim

        self.W_query = torch.nn.Linear(d_in, self.d_out, bias=False)
        self.W_key = torch.nn.Linear(
            d_in, self.num_kv_groups * self.head_dim, bias=False
        )
        self.W_value = torch.nn.Linear(
            d_in, self.num_kv_groups * self.head_dim, bias=False
        )

        self.out_proj = torch.nn.Linear(self.d_out, d_in, bias=False)

        if qk_norm:
            self.q_norm = RMSNorm(self.head_dim)
            self.k_norm = RMSNorm(self.head_dim)
        else:
            self.q_norm = None
            self.k_norm = None

    def forward(self, x, mask, cos, sin):
        batch_size, num_tokens, _ = x.shape

        # shape: (batch_size, num_tokens, num_heads * head_dim)
        queries = self.W_query(x)

        # shape: (batch_size, num_tokens, num_kv_groups * head_dim)
        keys = self.W_key(x)
        values = self.W_value(x)

        # shape: (batch_size, num_heads, num_tokens, head_dim)
        queries = queries.view(
            batch_size, num_tokens, self.num_heads, self.head_dim
        ).transpose(1, 2)

        # shape: (batch_size, num_kv_groups, num_tokens, head_dim)
        keys = keys.view(
            batch_size, num_tokens, self.num_kv_groups, self.head_dim
        ).transpose(1, 2)
        values = values.view(
            batch_size, num_tokens, self.num_kv_groups, self.head_dim
        ).transpose(1, 2)

        if self.q_norm:
            queries = self.q_norm(queries)
        if self.k_norm:
            keys = self.k_norm(keys)

        queries = apply_rotary_pos_emb(queries, cos, sin)
        keys = apply_rotary_pos_emb(keys, cos, sin)

        # shape: (batch_size, num_heads, num_tokens, head_dim)
        keys = keys.repeat_interleave(self.group_size, dim=1)
        values = values.repeat_interleave(self.group_size, dim=1)

        # shape: (batch_size, num_heads, num_tokens, num_tokens)
        attn_scores = queries @ keys.transpose(2, 3)
        attn_scores = attn_scores.masked_fill(mask, -torch.inf)

        # shape: (batch_size, num_heads, num_tokens, num_tokens)
        attn_weights = torch.softmax(attn_scores / self.head_dim**0.5, dim=-1)

        # shape: (batch_size, num_heads, num_tokens, head_dim) ->
        #        (batch_size, num_tokens, num_heads, head_dim) ->
        #        (batch_size, num_tokens, d_out)
        context = (
            (attn_weights @ values)
            .transpose(1, 2)
            .reshape(batch_size, num_tokens, self.d_out)
        )

        # shape: (batch_size, num_tokens, d_in)
        return self.out_proj(context)

2.4. FeedForward(SwiGLU)

前面Qwen3的整体架构图中也给出了FeedForward的结构，它由三个线性层组成，前两个线性层结构相同，分别对输入向量进行线性变换，得到第一个线性层的输出之后使用Silu激活函数，之后再与第二个线性层的输出两两相乘，结果送入第三个线性层，得到最终的输出。

class FeedForward(torch.nn.Module):
    def __init__(self, emb_dim: int, hidden_dim: int):
        super().__init__()
        self.fc1 = torch.nn.Linear(emb_dim, hidden_dim, bias=False)
        self.fc2 = torch.nn.Linear(emb_dim, hidden_dim, bias=False)
        self.fc3 = torch.nn.Linear(hidden_dim, emb_dim, bias=False)

    def forward(self, x):
        # shape: (batch_size, seq_len, hidden_dim)
        fc1 = self.fc1(x)
        fc2 = self.fc2(x)
        x = torch.nn.functional.silu(fc1) * fc2

        # shape: (batch_size, seq_len, emb_dim)
        return self.fc3(x)

2.5. MoE

MoE(Mixture of Experts)是一种混合专家模型，它将输入向量送入多个专家，每个专家都是一个FeedForward(SwiGLU)，在推理时会激活不同的专家，从而实现混合专家的计算并减少计算量。

class MoEFeedForward(torch.nn.Module):
    def __init__(
        self, num_active_experts: int, num_experts: int, emb_dim: int, hidden_dim: int
    ):
        super().__init__()
        self.num_active_experts = num_active_experts
        self.num_experts = num_experts
        self.emb_dim = emb_dim

        self.gate = torch.nn.Linear(emb_dim, num_experts, bias=False)
        self.experts = torch.nn.ModuleList(
            [FeedForward(emb_dim, hidden_dim) for _ in range(self.num_experts)]
        )

    def forward(self, x):
        batch_size, seq_len, emb_dim = x.shape

        # shape: (batch_size, seq_len, num_experts)
        scores = self.gate(x)

        # shape: (batch_size, seq_len, num_active_experts)
        topk_scores, topk_indices = torch.topk(scores, self.num_active_experts, dim=-1)
        topk_probs = torch.softmax(topk_scores, dim=-1)

        expert_outputs = []
        for i in range(self.num_experts):
            # shape: (batch_size, seq_len, emb_dim)
            out = self.experts[i](x)
            expert_outputs.append(out.unsqueeze(-2))
        # shape: (batch_size, seq_len, num_experts, emb_dim)
        expert_outputs = torch.cat(expert_outputs, dim=-2)

        # shape: (batch_size, seq_len, num_experts)
        gating_probs = torch.zeros_like(scores)
        for i in range(self.num_active_experts):
            # shape: (batch_size, seq_len, 1)
            indices = topk_indices[..., i : i + 1]
            prob = topk_probs[..., i : i + 1]

            # shape: (batch_size, seq_len, num_experts)
            gating_probs.scatter_(dim=-1, index=indices, src=prob)

        # shape: (batch_size, seq_len, num_experts, 1)
        gating_probs = gating_probs.unsqueeze(-1)

        # shape: (batch_size, seq_len, emb_dim)
        result = (gating_probs * expert_outputs).sum(dim=-2)

        return result

这里forward函数的操作比较复杂，这里详细介绍一下。

首先self.gate是一个线性层，输入是每个token的embedding向量，它的输出是对每个专家的打分，如果有4个专家，当前的token是apple，那么输出可能是

[2.1, 0.3, 1.7, -0.8]

表示专家0和2对这个token比较在行，下面

topk_scores, topk_indices = torch.topk(scores, self.num_experts_per_tok, dim=-1)

从打分中选出前self.num_experts_per_tok个专家，这里假设是2个，那么topk_scores和topk_indices是

topk_scores  = [2.1, 1.7]     # 分数
topk_indices = [0,   2]       # 选择专家0和专家2

topk_probs则将分数转化成权重

接下来会对每个专家的输出进行计算，并选择前self.num_experts_per_tok个专家的输出，下面这个循环中

    # shape: (batch_size, seq_len, 1)
    indices = topk_indices[..., i : i + 1]
    prob = topk_probs[..., i : i + 1]

    # shape: (batch_size, seq_len, num_experts)
    gating_probs.scatter_(dim=-1, index=indices, src=prob)

每次循环都会处理一个专家，假设我们有如下gate

topk_indices = [[[1, 3], [2, 0]]]
topk_probs = [[[0.7, 0.3], [0.6, 0.4]]]
num_experts = 4

要把topk_probs映射到完整的4个专家向量上，输出为

gating_probs = [
  [[0, 0.7, 0, 0.3],  # 第1个 token → Expert 1 和 3
   [0.4, 0, 0.6, 0]]  # 第2个 token → Expert 2 和 0
]

最后将gating_probs扩展维度与专家输出相乘并按照专家维度求和

  • expert_outputs.shape = (b, t, num_experts, emb_dim)
  • gating_probs.shape = (b, t, num_experts, 1)

3. 整体实现

现在我们已经实现了Qwen3的各个模块，接下来我们将使用这些模块来构建Qwen3模型:

import torch
from transformer import TransformerBlock
from rms_norm import RMSNorm
from rope import get_sin_cos


class Qwen3(torch.nn.Module):
    def __init__(self, cfg):
        super().__init__()

        self.token_embedding = torch.nn.Embedding(cfg["vocab_size"], cfg["emb_dim"])
        self.transformer_blocks = torch.nn.ModuleList(
            [
                TransformerBlock(
                    d_in=cfg["emb_dim"],
                    num_heads=cfg["num_heads"],
                    num_kv_groups=cfg["num_kv_groups"],
                    head_dim=cfg["head_dim"],
                    num_experts=cfg["num_experts"],
                    num_active_experts=cfg["num_active_experts"],
                    hidden_dim=cfg["hidden_dim"],
                )
                for _ in range(cfg["n_layers"])
            ]
        )

        self.final_norm = RMSNorm(cfg["emb_dim"])
        self.out_head = torch.nn.Linear(cfg["emb_dim"], cfg["vocab_size"], bias=False)

        if not cfg["head_dim"]:
            head_dim = cfg["emb_dim"] // cfg["num_heads"]
        else:
            head_dim = cfg["head_dim"]

        cos, sin = get_sin_cos(
            pos_seq_len=cfg["context_length"],
            dim=head_dim,
        )
        self.register_buffer("cos", cos, persistent=False)
        self.register_buffer("sin", sin, persistent=False)

        self.cfg = cfg

    def forward(self, x):
        x = self.token_embedding(x)

        num_tokens = x.shape[1]
        mask = torch.triu(
            torch.ones(num_tokens, num_tokens, device=x.device, dtype=torch.bool),
            diagonal=1,
        )

        for block in self.transformer_blocks:
            x = block(x, mask, self.cos, self.sin)
        x = self.final_norm(x)
        logits = self.out_head(x)
        return logits

不过这里我们只实现了Qwen3的模型结构，Qwen3模型比较大，需要足够的GPU资源才能进行训练，我没有GPU硬件，所以这里只是实现了模型结构，会使用较小的模型(比如GPT2)来实现训练和fine-tuning部分。

You may also enjoy

nano-vllm源码阅读 3: Scheduler

1 minute read

在前面文章中我们介绍了代表用户请求的Sequence类，以及负责管理block的BlockManager类。这篇文章将介绍负责调度Scheduler

nano-vllm源码阅读 2: Block Manager

3 minute read

在上一篇文章中，我们介绍了代表用户请求的Sequence类，它通过block_table来追踪存储其KV cache的物理内存块，这篇文章将介绍负责管理这些内存块的BlockManager类

nano-vllm源码阅读 1: Sequence

1 minute read

最近在学习 AI Infra 相关的知识并根据一些教程阅读nano-vllm的源代码，这里记录一下相关内容，我们从Sequence开始，因为在源码中它的dependency比较少，而且代表了用户的每一个请求

从零到一：用 Go 构建一个支持 MVCC 的内存数据库

1 minute read

在这篇文章中，我们将探讨如何使用 Go 语言从零开始构建一个功能强大的内存数据库。这个项目不仅仅是一个简单的键值存储，它还将支持事务、过期时间和并发控制的技术——MVCC（多版本并发控制）。